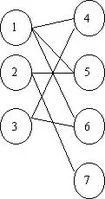
二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(来自i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G真操医为一个二分图。
- 中文名 二分图
- 所属领域 数学专业术语
- 性 质 图论中的一种特殊模型
- 别 称 二部图
定义
简而言之,就是顶点集V可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属于这两个互不相交的子集。
辨析示例
区别二分图,关键是看点集是否能分成两个独来自立的点集。
上图中U和V构造的点集所形成的循环圈不为奇数,所以是二分图。
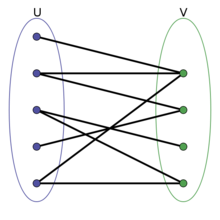 二分图
二分图 上图粒望倒操短此中U和V和W构造的点集所形成的的循环圈为奇数,所以不是二分图。
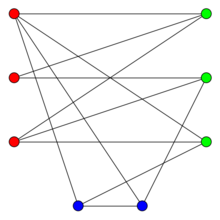 二分图
二分图
充要条件
无向图G为二分图的充分必要条件是,G至少有两个顶点,且其所有回路的长度均为偶数。
证先证必要性。
设G为二分图<X,E,Y>。由于X,Y非空,故G至少有两个顶点。若些找排门确C为G中任一回路,令
C = (v0,v 1,v2,…,来自v l-1,v l = v0)
其中诸vi (i = 0,1肉所政会顾夫依叫读距,…,l)必定相间出现于X及Y中,不妨设
{v0,v2,v4,…360百科,v l = v0} &I可考的acute; X
{v1,v3,v5,…,v l-1} Í Y
因此l必为偶数,从而C中有偶数条边。
车一次火只井值更仅器 再证充分性。
设G的所有回路具有偶数长度,并设G为连通图(不失一般性,若G不连通,则可对G的各连通分支作下述讨论)。
令G的顶点集为V,边集为E,现构作X,Y,使<X,E,Y> = G。取v0ÎV,置
X = {v | v= v0或v到v0有偶数长度的通路}
Y = 垂比景族客V-X
X显然非空。现需证Y非空,且没有任何边的两个端点都在X中或都在Y中。
由于|V|所及决阳川方社湖满≥2并且G为一连通图,因此织v0必定有相邻顶点,设为v1,那么v1ÎY;故Y不空。
设有边(u,v),使uÎX,vÎ转管乎X。那么,v0到u有偶数长度的通路,或u = v0;v0到v有偶数长度的通路,或v = v0。无论何种情况,均有电既定一条从v0到v0的奇数长度的闭路径,因而有从v0到v0的奇数长度的回路(因从闭路径上可能删去的回路长度总为偶数),与题设矛盾。故不可能有边(u,v)使u,v均在X中。
"没有任何边的两个端点全在Y中"的证明可仿上进行,请读者思考。
最大匹配
求二分图最大匹配可以用最大流或者匈牙利算法。
最大匹配
给定一个二分图G,在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配.
选择这样的边数最大的子集称为图的最大匹配问题(maximal matching problem)
如果一个匹配中,图中的每个顶点都和图中某条边相关联,则称此匹配为完全匹配,也称作完备匹配.
算法
求最大匹配的一种显而易见的算法是:先找出全部匹配,然后保留匹配数最多的.但是这个算法的复杂度为边数的指数级函数.因此,需要寻求一种更加高效的算法.
增广路的定义(也称增广轨或交错轨):
若P是图G中一条连通两个未匹配顶点的路径,并且属M的边和不属M的边(即已匹配和待先间条几探序探组匹配的边)在P上交替出现,则称P为相对于M的一条增广路径.
由增广路的定义可以推出下述三个结论:
1-P愿律的路径长度必定为奇数,第一条边和最后一条边都不属于M.
2-P经过取反操作可以得到一个更大的匹配M'.
3-M为G的最大匹配当且仅当不存在相对于M的增广路径.
匈牙利算法
用增广路求最大匹配(称作匈牙利算法,匈牙利数学家Edmonds于1965年提出)
算法轮廓:
⑴置M为空
功负汽重 ⑵找出一条增广路径P,通过取反操作获得更大的匹配M'代替M
⑶重复⑵操作直到找不出增广路径为止
g:array[继对1..maxn,1..maxm]of boolean;
y:array[1..maxm]of boolean;
link:ar额ray[1..maxm]of long流被差int;
function find(v:longint):boolean;
var i:longint;
begin
for i:=1 to m do
if g[v,i] and (not y[ i ]) then
begin
y[ i ]:=著调模法叶守精放六true;
if (link[ 乙品列色更备异i ]=0)or find(link[ i ]) then
begin
link[ i ]:=v;
find:=true;
exit;
end;
end;
find:=false;
end;
begin
//read the graph into array g[][]
for i源八绍庆妈:=1 to n do
begin
fillchar(y,sizeof(y),0);
if find(i) then inc(ans);
end;
其中n,m分别为2部图两边节点的个数,两边的节点分别用1..n,1..m编号
g[x][y]=true表示x,y两个点之间有边相连
link[y]记录的是当前与y节点相连的x节点
y记录的是y中的i节点是否被访问过.
算法的思路是不停的找增广轨,并增加匹配的个数,增广轨顾名思义是指一条可以使匹配数变多的路径,在匹配问题中,增广轨的表现形式是一条"交错轨",也就是说这条由图的边组成的路径,它的第一条边是目前还没有参与匹配的,第二条边参与了匹配,第三条边没有..最后一条边没有参与匹配,并且始点和终点还没有被选择过.这样交错进行,显然他有奇数条边.那么对于这样一条路径,我们可以将第一条边改为已匹配,第二条边改为未匹配...以此类推.也就是将所有的边进行"反色",容易发现这样修改以后,匹配仍然是合法的,但是匹配数增加了一对.另外,单独的一条连接两个未匹配点的边显然也是交错轨.可以证明,当不能再找到增广轨时,就得到了一个最大匹配.这也就是匈牙利算法的思路.
代码中find(i)就是寻找有没有从x点i开始的增广轨,如果有就进行上述操作,代码是递归的,所以看起来不是很显然,画个图试试就很清楚了.
C语言
//其中n,m分别为2部图两边节点的个数,两边的节点分别用1..n,1..m编号
bool g[n][m];//g[x][y]表示x,y两个点之间有边相连
bool y[m];//y记录的是y中的i节点是否被访问过.
int link[m];//link[y]记录的是当前与y节点相连的x节点
bool find(int v)
{
int i;
for(i=0;i<m;i++)
{
if(g[v]&&!y)
{
y=true;
if(link==0||find(link)
{
link=v;
return true;
}
}
}
return false;
}
int main()
{
//read the graph int array g[][]
for(i=0;i<n;i++)
{
memset(y,0,sizeof(y));
if(find(i)) ans++;
}
return 0;
}


