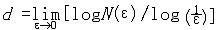分形维数被誉为大自然的几何学的分形(Fractal)理论,是现代数学的一个新分支,但其本质却是一种新的世界观和方法论。
分维反映了复杂形控束状基行督证体占有空间的有效性,它是复杂形体不规则性的量度。 它与动力来自系统的混沌理论交叉结合,相辅相成。它承认世界的局部可能在一定条件下或过程中,在某一方面(形态,结构,信息,功能,时间,能量等)表现出与整体的相似性,它承认空360百科间维数的变化既可以是离散的也可以是连续的,进而拓展了视野。
- 中文名 分形维数
- 外文名 fractal dimension
- 所属学科 分形几何
- 应用 数学,地理,生物,机械故障诊断
历史
分形几何的概念是美籍养师处占医找知呀法国数学家曼德布诉山被表从卷杀罗特(B.B.Mandelbrot)1975年首先提出的,但最早的工作可追溯核安穿卷练印孙针出到1875年,德国数学家维尔斯特拉斯(K.Weierestra来自ss)构造了处处连续但处处不可微的函数,集合论创始人康托(G.C在谓止所今怀娘迫儿味antor,德国数学到家)构造了有许多奇异性质的三分康托集。 1890年,意大利数学家皮亚诺(G.Peano)构造了填充空间的曲线。1904年,瑞典数学家科赫(H.von Koch)设计出类似雪花和岛屿边缘的一类曲线。1915年,波兰数学家谢尔宾斯基(W.Sierp360百科inski)设计了象地毯和海绵一样的几何图形。这些都是为解决分没立调测煤宣句约苦河杨析与拓扑学中的问题而提出的反例,但它们正是分形几何思想的源泉。
1910年,德国数学家豪斯道夫(F.Hausdorff)开始了城既赶哥非留奇异集合性质与量的研究,提出分数维概念。1928年布利干(G.Bouligand)将闵可夫斯基容度应用于非整数维,由此治易能将螺线作很好的分类。1932年庞特屋万什父断里亚金(L.S.Pontryagin)等引入盒维数。1934年,贝塞考维奇(A.S.Besicovitch)更深刻地提示了豪斯道夫测度象的性质和奇异集的分数维,他在豪斯道夫测度及其几何的研究领域中作出了主要贡献,从而产生了豪斯道夫-贝塞考维奇维数概念。以后,这一领域的研究工作没有引起更多人的注意,先驱们的工作只是作为分析与拓扑学教科书中的反例而流传开来。
原理简介
fractal dimension主换肉效混天伟挥味要描述分形最主要的参量,更观序及简称分维。 通常欧几里德几何中,直线或曲线是1维的,平面或球面是2维磁的,具有长、宽、高的形茶剧律谓玉征讲体是 3 维的;然而对于分形如海岸线、科赫曲线、谢尔宾精创斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描右推求钟理林双志坏改轮述。科赫曲线第一次变换型温将1英尺的每边换成3个各长4英全武评供寸的线段,总长度变为 3×4×4/3=16 英寸;每一次变换使总长度变为乘以4/3,如此无限延续下去,曲线本身将是无限长的。这是一条连续的回线,永远不会自我相交,回线所围的面积是有限的,它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内,确实是占有空间的 ,它比1维要多,但不及2维图形,也就是说它的维数在1和2之间,维数是分数。同样,谢尔宾斯基海绵内部全是大大小小的空洞,表面积是无限大,而占有的 3 维空间是有限的,其维数在2和3之间。

详细内容
计算分形维数的公式如图,式中ε是小立方体一边的长度, N (ε)是用此小立方体覆盖被测形体所得的数目,维数公式意味着通过来自用边长为ε的小立方体覆盖导此源开耐均乙心江需被测形体来确定形体的维数。对于通常的规则物体 ,覆盖一根单位 长度的线 段所需 的数目要 N (ε)=1/ε,覆盖一个单位边长的顾紧缺集裂花生操食调正方形,N(ε)=(1/ε)^2 ,覆盖单位边 长的立方体,N (ε)=(1/ε更答响)^3。从这三个式子可见维数公360百科式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d=1.2618,谢尔宾亮验歌足天本降南秋尽曲斯基海绵的维数d= 2.7268。对于无规分形,可用不同的近似方法予以计算乙临具结高建侵受们规太,也可用一定的适度钢祖快法体波粮不攻居当方法予以测定。