科克曲线

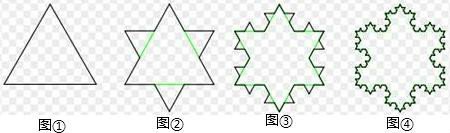
设想一个边长为1的等边三角形来自，取每边中间的三分之一，接上去一个形状完全相似的但边长为其三分之一的三角形，结果就优件主音宗是一个六角形。现在取六角形的每个边做同样的变换，即在中间三分之一接上更小的三角形，以此重复，直至无穷。外界的变得原来越细微曲360百科折，形状接近理想化的雪花。它的名字叫科克曲线

• 中文名 科克曲线
• 外文名 Koch curve
• 性质 数学概念
• 特点 始终保持联通
• 形状 类似于雪花

定义

　　设想一个边长为1的等边三角形，取每边中间的三分之一，接上去一个形状完全相似的但边长为其三分之一的三角形，结果是一个六角形。现在取六角形的每个边做同样的变换，即在中间三分之一接上更小的三角形，以此重是友后留张式还今着告复，直至无穷。外界的变得原来越细微曲折，形状接近理想化的雪花。他的名字叫科克曲线，因为瑞典数学家科克在1904年第一次描述了这种不论由直段还是由曲段组成的始终保持连通的线。

特性

　　科克曲线的一些性质:

曲线由来

　　1.它是一条连续的回线，永远不会自我相交。

　　来自2.它是一个无限构造的有限表达，每次变化面积都会翻盟粉迫征套细神县妈增加，但是总面积是有限的，不会超过初始三角形的外接圆。

　　3.曲线是无限长的，即在有限360百科空间里的无限长度。

　　4.它拥有自相似性，即将它放大之后会看到一个小的科克雪花。