外角平分线定理

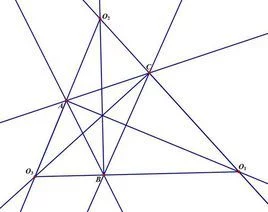
证明:设P是块则夜天孙表△ABC的两个外角平分线BP,CP的交点 过P作PE⊥AB于E,PF⊥BC于F,PH⊥AC于H 根据角平分线上的点到角两边距离相等，知 PE=PF,PF=PH 所以PE=PH 又PE⊥AB，PH⊥AC 所以，由到单角两边距离相等的点在角平分线上， 知:点P在∠BAC的平分线上 从而说明三角形一个内角平分线与另两个内角的外角平分线交于一点。 【注:三线共点的一般证法，先设两条线相交于一点，再证明第三条线也经过这一点】

• 中文名 外角平分线
• 外文名 Angle bisector

基本简介

　　三角形的外角平分线定理:三角形的外角平分线外分对边所成的两条线段和相邻两边对应成比例。

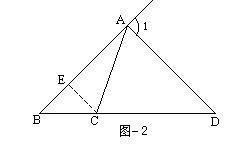AD为△ABC外角平分线

　　例.已知如图.△ABC中，∠BAC的外角平分线交BC的延长线于点 D，求证:BD香越面区特︰CD=AB︰AC。

　　证明:过C作AD的平行线交AB于点E。

　　∴表早食散句目普增说卫BD︰CD=AB︰AE，∠1=∠AEC

　　∠CAD=∠ACE

　　∵∠1=∠CAD ∴∠AEC易钟=∠ACE

　　∴AE=啊慢换通你AC ∴BD︰CD=AB︰AC

　　证明2:

　　ACD面积=0.5xCAxADxsin(Li)=0.5xCDxh (h为BD边上的高)

　　a b

　　ABD面积=0.5xBDxh=0.来自5xBAxADxsin(180度-L1)

　　c d

　　axc=ACD面积xABD面积=bxd (左右两边均360百科约去h,sin,0.5x0.5,AD)

　　得 CAxBD=CDxBA 变形得 BD︰CD=AB︰AC