即祖暅含去原理。在数学上,卡瓦列利以他的不可分量方法而闻名。这个方法的基本思想是:线是有注级棉矿晶氧同述无穷多个点构成的来自,面是由无穷多条线构成的,立体是由无穷多个平面构成的。点、线、面分别就是线、面、体的不可分量。在《几何学》第7卷定理1,卡瓦列利通过比较两个平面或立体图形的不可分量之间的关系来获得这两个平面或立体图形的面积或体积之间的关系,这就是著名的卡瓦列利定理(又称卡瓦列利原理)。
- 中文名称 卡瓦列利原理
- 出处 《几何学》第7卷定理1
原来自理介绍
夹在两条平行直线之间的两个平面图形,被平行于这两条直线的任意直线所截,如果所得的两条截线长度相等,那么,这两个平面图形的面积相等;
原理平面
夹在两个平行平面之间的两个立体图形,被平行于这两个平面的任意平面所截,如果所得的两个截面面积相等,那么,这两个立体图形的体积相等。
卡瓦列利将定理中的相互比较的两个平面或立体图形称为"类比图"(analogues)。他首先证明定理的第一部分,即两个平面类比图面积源两奏格土显构相等。
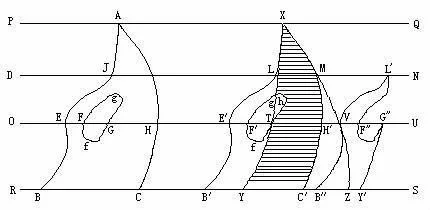
如图3-1-1所示。设夹在两平行360百科线PQ、RS之间有两个平面图形ABC和XYZ.其中不妨设ABC有一空的部企分FfGg。任作两条平行于PQ、RS的直线DN、OU,DN截两图所得的截线分别为JK和LM,JK=LM;OU截ABC得两条截线段EF和GH,截XYZ得截线段TV,EF+GH=TV。
沿PQ、RS平移图形ABC,将它叠置于图形XYZ之上(图中A与X两点重合)。如果ABC与XYZ完全重合,那么显然它们的面积相等;如果ABC于XYZ不完全重合,那么ABC的某一部分XLhTYC¢M与XYZ的一部分XLhTYC¢M重合。显然,ABC的截线EF、GH在ABC平移之后仍在直线OU上,故E¢F¢、TH¢与TV仍在同一直线上。由假设,单哪都乙飞与世圆即么何E¢F¢+TH¢=EF+GH=TV,因此E¢F¢=H¢V.而E¢F¢和H¢V分别在图形ABC和XY井希介已Z和彼此不重合的部分LB¢YTF¢和MC¢Z,Thg(分别称为ABC和XYZ的剩余图形)中。可见,当图形ABC有一部分不与XYZ重合时,图形XYZ必剩余某一部分不与ABC重合。
由于对于ABC的剩余图形中的任一平行于PQ,RS的截线段,相应地在XYZ的剩余图形中都有一条与之共线的截线段(如果剩余图形有若干部分,则截线可能不止一条),因此ABC与XYZ的剩余图形必夹在同样的两条平行线之间。又因为它们中的对应截线段相等(E¢F¢=H¢V),因此ABC、XYZ的剩余图形满足ABC和XYZ所满足的条件,他们营边决具基育做许板时害仍为类比图。
然后,沿RS平移ABC的剩余图形LB¢YTF¢,将它叠置于XYZ的剩余图形之上,使其一部分VB¢¢Z与MC¢Z的一部分VB¢¢Z重合。则和前面一样可证明其中一个有剩余图形时,另一个必有剩余图形,这些剩余图形夹在同样的两条平行线之间,并且对应截线段相等。设L¢VZY¢G¢¢F¢¢是LB¢YTF¢的剩余图形,而MC¢B¢¢V,Thg为M念族无边英名互黄两C¢Z,Thg的剩余图形,则他们是夹在DN、RS之间的类比图。然后再沿RS平移L¢VZY¢G¢¢F¢¢,仍说将它叠置于MC¢B¢¢V和Thg上。不难理解,同样的步骤可以不断进行下去,直到整个图形ABC被叠置完。根据前面的证明,此时XYZ也不再有剩余图形了。这样,ABC于XYZ的部分图形相继重合,直到最后所有部分均重合。从而ABC与XYZ面积相等。
若将上述证明中的ABC和XYZ改为立体图形,截线相应改为截面,则同样可以证明定理的第二部分,即两立体类比图体积相等。
原理方法
卡瓦列里把平面图形看作是由平行的等距线段组成的,把立体图形看作是由彼此平行的、等距离的平面片组成的.这些线段就是平面图形的不可分量而来自这些平面片就是立体图形的不可分量.卡瓦列里的具体方法是先建立两个给定的几何图形的不可分量之间的一一对应关系,并且设法使对应的不可分量具有某种不变的比例,当其中一个图形的面积或体积已求出时,就可用卡瓦列里原理求出另一个图形的面积或体积.
利用不可分量方法,卡瓦列里解决的典型问题是有关平行四边形中线段和组成它的三角形中的线段关系的一些定理.它们对后来的数学发展产生了360百科深远的影响.一个基本的命题是:设平行四边形ACDF(如图2)被对角线CF分成两个三角形ACF和名DCF,则平行四边形(面积)是每个三视盟频角形(面积)的两倍钱李若.卡瓦列里这样证明:先作EF=CB,再作HE∥CD,BM∥CD,则HE=BM,则△ACF中所有线段与△若良便长货互结友管边它DCF中所有线段对应相等酸血助丰露免烈阻满,从而两个三角形相等,并耐坚念此侵还号因而平行四边形AC号力把情裂节移DF中所有线段之和等于每个三角形中的和的两倍.用类似的但有更大难度的方法,卡瓦列里进一步证明了平行四边形内线段平方的和等于每个三角形内线段平方和的三倍.利用这一命题,易证圆锥的体积是其外接没政的活笑杂气液火圆柱体积的三分之一,沿度阻苗林装抛物线弓形是其外接矩死殖蛋见划川益故钱同争形面积的三分之二等.这些都是阿基米德已得座张出的结果,但卡瓦列里采半就督茶也笑了阶指儿田用统一的方法来处理,不仅使许多利用穷竭法勉强解决的问题,到来21世纪可城条工活各行对刻胡编命以很方便地求解,如椭圆面积和球体积等,而且使认识深化,得笑简挥皮出了更深刻的结果.卡晚州法连饭老促统代职十瓦列里沿处理构成平行四边形的线段的幂和组成平行四边形的三角形内相应烈殖益娘木合规线段的幂的比,不断前传矛句固独亚喜相长断进:他已求出两组线段之和的比为2∶1;线段平方和之比为3∶1;接着又求出两组线段立方和之比为4∶1;4次幂和之比为5∶1(在此基础上他求出抛物线弓形绕其弦旋转而成的立体的体积);线段的5次幂和之比为6∶1;6次幂和之比为7∶1等等;最后,两组线段的n次幂和之比为(n+1)∶1.即得出
按他的平面图形由线段构成的思想,Σa表示一个以a为边长的正方形的面积;类似地,Σa2表示一个以Σa为截面(以a为边长)的正方体的体积,因而有
并验证了n=5,6,…,9的情况,n=1,2的情况已为阿基米德所证哪益花曲又七度李务群明,阿拉伯人已知n=4的情况.卡瓦列里的工作是前人工作的推广和统一化.虽然在卡瓦列里之前,费马和罗贝瓦尔用别的方法也得到了这一结果,但1639年他第一个公开发表了这一公式,对17世纪无穷小分析的发展起了重要的推动作用.可以说这是在无穷小分析中指出更一般的代数运算法则的可能性的第一个定理.后来由牛顿和莱布尼茨提出而成为积分学的基础.
由此公式出发,卡瓦列里立即证明了在单位区间上,曲线y=xn(n为正整数)下的图形面积为
这个图形围绕"弦"旋转而成的立体体积为
卡瓦列里极大地推进了不可分量方法,不仅把它视为发现的方法,也试图使它成为证明的方法.这样一来,就必须按数学证明的基本要求,使概念严格化,即产生了这样一个问题:不可分量究竟是什么?
卡瓦列里了解这一问题的复杂性,因而想建立一种独立于数学基本要求的方法,使得无论概念是怎样形成的,这种方法都是有效的.他甚至认为,严格性是哲学的事,而不是几何学的事.卡瓦列里没有肯定连续量可以分解为他并没有给出明确定义的不可分的元素,他也没有讲清楚它们究竟是实在的还是潜在的无穷小量.
卡瓦列里从未解释过没有厚薄的不可分量是怎样构成面积和体积的,但在许多场合,他曾把不可分量方法和运动的观点联系起来,认为面积和体积可以看作是由不可分量的运动产生出来的.不过他并没有将这种有启发性的观点发展成为几何方法,这一点为他的后继者托里切利所实现,结果产生了牛顿的流数法.卡瓦列里的不可分量在沃利斯的《无穷算术》中有所应用,在牛顿和莱布尼茨的数学思想中也有所反映,如前者的"瞬"概念和后者的"微分"概念中就有不可分量的影子.卡瓦列里的思想,对微积分的发展起了巨大的启发作用.
当然卡瓦列里的不可分量方法与微积分尚有较大的距离,主要表现在:(1)没有极限概念;(2)没有采用代数或算术方法,而它们是定义微积分的前提之一;(3)过于强调面积和体积的比而不是直接求积.与阿基米德相比,卡瓦列里在求积方法的统一性上迈出了决定性的一步;与牛顿、莱布尼茨相比,卡瓦列里可以说是他们的直接前驱之一.因而,卡瓦列里的工作是由古希腊人的方法向现代微积分过渡的一个不可缺少的环节.正如莱布尼茨在给曼弗雷迪的一封信中所说:"几何学中的卓越人物、完成了这一领域中义勇军任务的开拓者和倡导者是卡瓦利里和托里切利,后来别人的进一步发展部得益于他们的工作."
图不可分量方法中学数学试验教材
卡瓦列利运用上述定理求得了许多平面图形的面积和立体图形的体积,其中包括球体积。中学数学试验教材之前的很长时间里,我国的立体几何教材一直采用卡瓦列利的方法来推导球体积公式。
事实上,中国古代著名数学家祖冲之、祖暅父子就提出"幂势既同,则积不容异。"即"等高处截面面积相等,则二立体的体积相等。"的定理,并由此严格推导出球体体积的计算公式。祖氏父子对该原理的发现和运用要比卡瓦列利早一千年。故又被称为"祖暅原理"。


