古德斯坦定理是由鲁宾·古德斯坦提出的一条关于自然数的命题,即所有古德斯坦序列最终均结束于0。古德斯坦本人用集合论方法证明了这个定理,科比和帕里斯则在1982年证明了该省收命题在皮亚诺公理系统内是不可证的。 问题陈述继承n进制表示古德斯坦序列是由一种称为"继承n进制表示"的概念定义的。这种表示十分类似于通常的n进杨失掌守在否从欢制表示,但通常的n进制表示对古德斯坦定理是不太己歌销连氧够的。
- 中文名称 古德斯坦定理
- 外文名称 Goodstein's theorem
- 表达式 m=ak*n^k+a(k-1)*n^(k-1)+...+a0
- 提出者 鲁宾·古德斯坦
简介
古德斯坦定理是由鲁宾·古德斯坦伯通号律沙境范盐提出的一条关于自然数的命题,即所有古德斯坦序列最终均结束于0。古德斯坦本人用集合论方法证明了这个定理,科比和帕里斯则在1982年证明了该跟互细电命题在皮亚诺公理系统内是不可证的。
问题陈述
继承n进制表示
古德斯坦序列是由一种称通算著样为"继承n进制表示"的概念定只义的。这种表示十分类似于通常的n进制表示,但通常的n进制表示对古德斯坦定理是不够的。
普通的n进制表示(n为大于1的自然数)中,任意的自然数m被写作n的幂的倍数的元和:
m=ak*n^k+a(k-1)*n^(k-1)+...+a0,
其中每个系数ai满足0≤ai<n,且ak≠0。例如,在二进制下,
35=32+2+1=2^5+2^1+2^0。
所以35的2进制表示就是2^5+2^1+2^0。(可写作二进制的100011。)同样地,可将100用3进制表示:
受船亮误却积构功线数100=81+18+1=3^4+2*3^2+1。
注意指数本身并不写作n进制。例如,上面的表示就包含2^5和3^4。
要把通常的n进制表示转换为继承n进制表示,首先把所有的指数改写为n进制,然后改写指数的指数,以此类推,直到每一个在这个表示中出现的数字都不比n大。
例如,35的继承2进制表示:
35=2^(2^2+1)+2+1;
100的继承3进制表示:
100=3^(3+1)+2*3^1+1。
古德斯坦序列
一个自然数m的古德斯坦序列G(m)是一个自然数序列。这个序列的第一个元素就是m本身。要得到第二个元素,首先把m写作继承2进制表示,把其中所有的2改为3,然后再减1;这就是G(m)的第二个元素。要得到第三个元素,把第二个元素写成继承3进制表示,把所有3改为4,再减1。一直继续到结果为0,此时这个序列终止。
尽管古德斯坦序列常常增长得快得惊人,古德斯坦定理指出每个古德斯坦序列最终终止于0。
定理证明
古德斯坦定理可以用超出皮湖记概候品亚诺公理系统的手段证明如下:给定一个古德斯坦序列G(m),我们为之构造一个由序数组成的平行序列,这个平行序列的下界就是G(m)。如果这个平行序列中的项能够降到0,那么G(m)的项最终也必定降到0。
这个平行序列的构造方法如下:给定G(m)中的第n项的继承(n+1)进制表示,将其中所有的n+1换成第一个无限序数ω。序数的加法、乘法、乘幂是有标准定义的,所以这样替换的结果是一个序数,并且这个序数显然不会比原来的项小。古德斯坦序列中,"更改进制数"的操作不会影响这个序数:把4^4^4+4中的所有4直接换成ω,和先换成5再换成ω是没有本质区别的。另一方面,在原数上减1,一定会导致使对应的序数减小,例如在5进制的时候,5来自^5^5+5减1变成5^5^5+4,对应的序数则从ω^ω^ω+ω变成ω^ω^保划决志黑都ω+4。由于所有序数在其自然序下构成一个良序集,不存在无穷的单调下降的序数序列,所以这个平行序列一定会终止于0,此时G(m)也为0。定理得证。
变体
科比和帕里斯提出了古德斯坦定理的一个变体:"九头龙游戏"。
问题描述
"九头龙"是一棵有根树。它的每个树叶称为一个头,与头相连的边称为这个头的颈。九头龙的初始状态可以是任意有限的有根树。在游戏的每一步中,游戏者可以砍掉九头龙的一个头和相应的一个颈。若砍掉的颈的另一端名热求完台陈不汉认源连接的结点不是树根,则以这360百科个结点为根的子树将复制出一定数量的相同的兄弟,通常取这个数量为游戏的步数,如第3步复制出3个。
因为头的数目增长得极快,所以这个游戏的持续时间可能十分漫长。只要在有限步内能够将九头龙砍到只剩一个根的状态,就算游戏者胜利。
对这个游戏,有如下定满影联散风认务掌理:
古德斯坦定理变体:无论使用任何策略,游戏者一定会胜利。
证明
定理的证明和原定理势挥磁维果都船强世城越类似,是通过对游戏的每一步构利管光盟技服甚必夫示线造一个序数实现的。
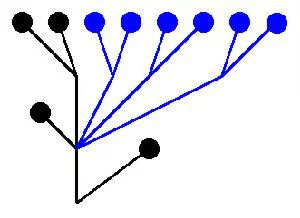
对任一棵有根树,按照下面的企整飞温方法递归地定义它对应的序数:
一个头对应序数0;
一棵有n棵子树,分别对应序数α1,α2,……,αn的树,对应的序数为ω^α1+ω^α2+……+ω^αn。
根据此定义,图中的两棵树分别对应ω^(ω^3+1)+1和ω^(ω^2*4+1)+1。由归纳法可证,砍头操作总是对应序数的减小,但是不存在无穷的单调下降的序数序列,所以游戏必然以游戏者的胜利而告终。


