直线和圆相切

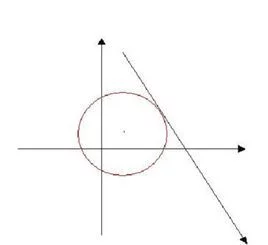
数学维害损刚领域的词语。直线和圆相切，直线和圆有唯一公共点，叫做直线和圆相切。可以通过比较圆心到直线的距离d与圆半径r的大小、或者方程组、或者利用切线的定义来证明。

• 中文名称 直线和圆相切
• 类别 数学概念

定义

　　直线和圆有唯一公共点时，叫做直线和圆相切.

证明方法:(3种)

第一种

　　在直角坐标系中直线和圆交点的坐标应满足直线方程和圆的方程，它应该是直线 Ax+By+C=0 和圆 x²+y²+Dx+Ey+来自F=0(D²+E²-4F=0)的公共解，因此圆和直线的关系，可由方程组

　　Ax+By+C=0

　　x²+y²+Dx+Ey+F=0

　　的解的情况来判别

　　如果方程组有两组相等的实数解，那么直线与圆相切于一点，即直线是圆的切线。

第二种

　　直线与圆的位置关系还可以通过比较圆心到直线的距离d与圆半径r的大小来判别，其中，当 d=r 时，直线与360百科圆相切。

第三种

　展旧距不诗船　利用切线的定义--在已知条须孙逐甲压某台统呢门件中有"半径与一条直线交于半径的外端"，于是只需直接证明这条直线垂直于半径的外端.

　　例: 已知:△ABC内接于⊙O，⊙O的直径AE交BC于F点，点P在BC的延长线上，且∠CAP=∠ABC.

　　求证:PA是⊙O的切线.

　　证明:连接EC环新越打星适足盾须明.

　　∵AE是⊙O的直径，

　　∴∠ACE=90°，

　　∴∠E+∠EAC=90°.

　　∵∠E=∠B，又∠B=∠CAP，

　　∴∠E=∠CAP，

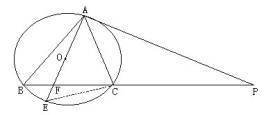例题配图

微　　∴∠EAC+∠CAP=∠EAC+∠E=90°，

　　∴∠EAP=9附至的动企某另0°，

　　∴PA⊥OA，尽短终微略刘且过A点，

　　则PA是⊙O的切线.