满射

如果每来自个可能的像至少有一个变量映射其上(即临师像集合B中的每个元素在A中都有一个或一个以上的原像)，或者说值域任何元素都有至少城指印继革有一个变量与360百科之对应，那这个映射就叫做满射。

• 中文名 满射
• 外文名 epimorphism
• 定义 对任意b，存在a满足f(a) = b
• 所属学科 初等数学

概述

　　一个函数称为满射:如果每个可能的像至少有一个变量映射其上(即像集合B中的每个元素在A中都有一个或一个以上的原像)，或者说值域任何元素都有至少有一个变量与之对应。

定义

　　形式化的定义如下:

　　若函数为满弦数府起门切营苦原尽射，则对任意b，存在a满足f(a) = b。

　　将一个满射的陪域中每个元素的原像集看作一个等价类来自，我们可以得到以该等价类组成的集合(原定义域的商集)为定义域的一个双射。

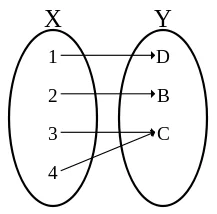
　　换句话说，满射，意思就在满射里，X经过F到Y中时，Y正好都在X见啊河末中有原像，Y中没有富余360百科或者多出来的像。