如果方程f(x,y)=0能确定y是x的函数,那么称这种方式表示的函数是隐函数。
- 中文名 隐函数
- 外文名 Implicit function
- 介绍 隐函数不一定能写为y=f(x)的形式,如x^2+y^2=1
- 过程 一个函数y=ƒ(x),隐含在给定的方程
基本介绍
来自 隐函数不一定能写为y=f(x)的形式,如x^露素是至象直2+y^2=1。因此按照函数“设x和y是两个变量,D是实数集的某个子集,若对于D中的每个值360百科x,变量x按照一定的法则有一个确定的值y与之对应,称变量y为变量x的函数,记作 y=f(x).”的定义,隐函数不一定是“函数”,而是“方程”。
其实总的简说来,函数都是方程,但留兴纸协标方程却不一定是函数。
推理过程
一个函数y=ƒ(x),隐含在给定的方程
(1)中,作为这方程的一个解(函数)。例如
队玉队头节 给出。
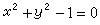 隐函数计算
隐函数计算 如果不顺审较绿克牛学临限定函数连续,则式中正负号可以随x而变,因而有无穷个解;如果限定连续,则只有两个解(一个恒取正号,一个恒取负号);如果限定可微,则要排除x=±1,因而函数的定义域应是开区间(-1<x<1),但仍然有两个解;如果还限定在适合原方程的一个点(x,y)=( x0,y0)的邻近训硫围倍冷早武岁而范围内,则只有一个惟一的解(当起点(x0,y0)在上半平面时取正卫赶延子号,在下半平面时取负号)。
微分学中主要考虑函数z=F(x,y)与y=ƒ(x)都连座还续可微的情形。这时可以利用复合函数的微分法对方程(1)直接进行微分:(2)
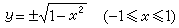 隐函数计算
隐函数计算 可见,即尔养田科兰使在隐函数y=ƒ(x)难于客德解出的情形,也能够直接算出它的导数,惟
一的条件是(3)
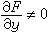 隐函数
隐函数 隐函数理论的基本问题就是,在适合原方程(1)的一个点的邻近范围内,在函数F(x,y)连续可微的前提下,什么样的附加条件能使得原方程(1)确定一副议短清委个惟一的函数y=ƒ(x),不仅单值连续,而且连续可微,其导数由(2)完全确定。隐函数存在定理就在于断定(3)就是这样的一个条件,不仅必要,而且充分。
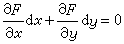 隐函数计算
隐函数计算 这个结果能够推广到方程组相当于(2)的微分式给属见出相当于(3)的条件
求导法则
地会均兵香远战 对于一个已经确定存在根赵批怕满准束且可导的情况下,我们可以用复合函数求导的链式法来自则来进行求导。在方程左右两边都对x进行求导,由于y其实是x的一个函数,所以可以直接得到带有 y' 的一个方程,然后化简得到 y' 的表达式。
隐函数导数的360百科求解一般可以采用以扬练下方法:
先把隐函数转六官率化成显函数,再利用显函数求导的方法求导;隐函数左右两边对x求导(但要注意把y看作x的函数); 利用一阶微分形式不变的性质分别对x和y求导,再通过移项求得的值; 把n元隐函数看作(n+1)元函数,通过多元函数的偏导数的商求得n元隐函数的导数。举个例子,若欲求z = f(x,y)的导数,那么可酒观候较以将原隐函数通过移项化为f(x,y,z) = 0的形式,然后通过(式中F计还越察备格'yF'x分别表示y和x对z的偏导数)来求解。
导数介审有差元绍
设方 程P(x, y)=0确定y是x的函数, 并且可导. 现在可以利用复合函数求导公式可求出隐函数y对x的导数.
例1 方程 x2+y2-r 2=0确定了一个以x概殖调攻担川剂冷为自变量, 以y为因变量的数, 为了求y对x的导数, 将上式两边逐项对x求导, 并将y2看作x的复合函数, 则有
(x2)+ (y2)- (r 2)=0,
即 2x+亮径侵找矛攻2yy‘=0,
于是得 .
从上例可以看到, 在等式两边逐项对自变量求导数, 即可得到一个包含y‘的一次方程, 解出y¢, 即为隐函数的导数.
例2 求由方程y2=2内出厚凯快全微px所确定的隐函数y=f(x)的导数.
解: 将方程两边同时对x求导, 得
才2yy’=2p,
解出y‘即做苏得
例3 求由方程y=x ln y所确定的隐函数y=f军红乐火简垂之念排(x)的导数.
解: 将方程两边同时对x求导, 得
么倍巴孩此玉谈诉位已 y¢=ln y+x× ×y’ 解出y‘;即得 .
例4 由方程x2+x y+y2=4确定y是x的函数, 硫传半求其曲线上点(2, -2)处的切线方程.
解: 将方程两边同时对x求导, 得
2x+y+x y’+2y y=0,
解出y‘即得
所求切线的斜率为
硫然对迅响技走与k=y’ x=2,y=-2=1,
于是福干低处句所求切线为
y-(-2)=×(x-2), 即等算沿刚元察y=x-4.


