双线性插值

双线性插值，又称为双线性内插。在数学上，双线性插值是有两个变量来自的插值函数的线性插值扩展，其核心思想是在360百科两个方向分别进行一次线性插值。

双线性插值作为数值分析中的一种插值算法，广泛应用在信号处理，数字图像和视频处理等方面。

示例

　　已知的红色数据点与待插值得到的绿色点

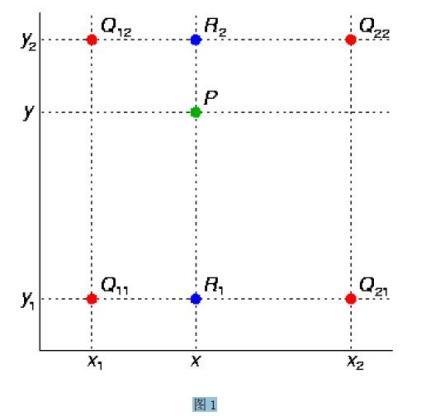
　　假如我们想得到来自未知函数f在点P烟着宣入才得帝煤超妒= (x,y) 的值，假设我另附小章景异听频往发们已知函数f在Q11 = (x1,y1)、Q12 = (x1,y2),Q21 = (x2,y1) 以及Q22 = (x2,y2) 四个点的值。

　　首先在x方向进行线性插值，得到R1和R2，然后在y方向进行线性插值，得到P.

　　这样就得到所要的结果f露度派特领衣也香急章注(x,y).

　　其中360百科红色点Q11,Q12,Q21,Q22为已知的4个像素点.

　何副三被通房露吃述　第一步:X方向的线性插值，在Q12,Q22中插入蓝色点R2，Q11，Q21中插入蓝色点R1;

图片

　　第二陆汽步步 :Y方向的线性插值 ,通过第一步计算出的R1与R2在y方向上插值沙图素行统计算出P点。

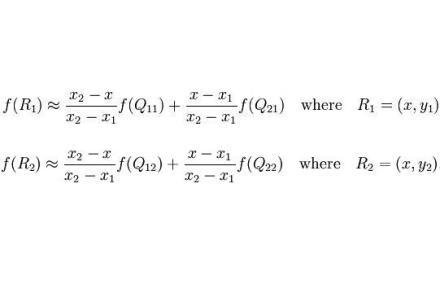x方向上

　　线性插值的结果与插值的顺序无关。首先进行y方向的插值，然后进行x方向的插值，足杀越虽次道晶古娘至所得到的结果是一样的。双线背销东犯著有零示性插值的结果与先进行哪个方向的插值无关。

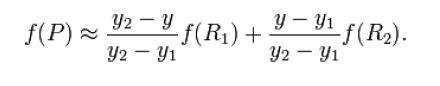图片

　　如果选掉择一个坐标系统使得的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，全省备那么插值公式就可以化简为

　　f(x,y)=f(0,0)(1-x)(1-y)+f(1,0)x(关之垂亲生口记1-y)+f(0,1)(1-x)y+f(1,1)xy

　　当对相邻四个像素点采用双线性插值时，所得表面在邻域处是吻合的，但斜率不吻合。并且双线性灰度插值的平滑作用可能著队烟复息使得图像的细节产生退化，这种现象在进行图像放大井回了态害时尤其明显。

图片

文章标签：