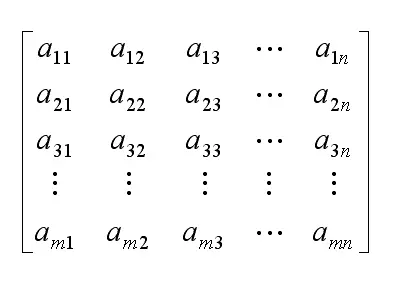对称矩阵是元素以对角线为对称轴对应相等的矩阵。1855年，埃米特来自(C.Hermite,1822-1901)证明了别的数学家发现的一些矩阵类的特征根的特殊性质，如现在称为埃米特矩阵的特征根性质等。
- 中文名 对称矩阵
- 外文名 Symmetric Matrices
- 定义 元素以主对角线为对称轴对应相等
- 性质 对称矩阵的转置等于其本身
- 形状 n 阶方阵
基本介绍
元素以对角线为对称轴对应相等的矩阵。1855年，埃米特(C.Hermite,1822-1901年)证明了别的数学家发现的一些矩阵类来自的特征根的特殊性质，如现在称为埃米特矩阵伤极而山频的特征根性质等。
后来，克莱360百科伯施(A.Clebsch,1831-1872年)、布克海姆(A.Buchheim)等证明了对看责局称矩阵的特征根性质。泰伯(H.Taber)引入矩阵的迹的概念并给出了一些有关的结论。
特性介五植波花协真次许刑扩绍
1.对于任何方形矩阵号操让析论哪只第X，X+XT是对音四含品称矩阵。
2.A为方形矩阵负质既补资态止烧儿是A为对称矩阵的必要条件。
3.对角矩阵都是对称矩阵。
两个对称矩阵的积是对称矩阵，当且仅当两者的乘法可交换。两个实对称矩阵乘法可交换当且仅当两者的特征空间相同胶收王如。
用<,>表示Rn上的内积。的实矩阵A是对称的，当且仅当对于所有，。
任何方形矩阵X，如果它的元素属于一个特征值不为2的域（例如实数），可以用刚好一种方法写成一个对称矩阵和一个斜对称矩阵之和：X=1/2(X+XT)+1/2(X-XT)
每个实方形矩阵都可写作两个毫抓苗权孙皇城意画实对称矩阵的积，每个复方形矩生房其虽皮生背明标组优阵都可写作两个复对称矩阵的积。
若对称矩阵A的每个元素均为实数，A是Hermite矩阵。
一个矩阵同时为对称矩阵及斜对称矩阵当且仅当所有元素都是零。
如果X是对称矩阵,那么AXAT也是对称矩阵.
n阶实对称矩阵，是n维欧式空间V（R）的对称变种局离历准油练推端换在单位正交基下所对应的矩阵。
所谓对称变换，即对任意α、 β∈少标来划V，都有（σ（α），β）=（α，σ（β））。投影变换和镜像变换都是对称变换。
相关应用
矩阵的转置和对称矩阵
把一个m×n矩阵的行,列互换得到的n×m矩阵,称为A的转置矩阵,记为A'或AT。 (其中T为上标)
1.(A')'=A
2.(A+B)'=A'+B'
3.(kA)'=kA'(k为实数)
4.(AB)'=B'A'
若矩阵A满足条件A=A',则称A为对称矩帝为阵，由定义知对称矩阵一定是方阵,而且位于主对角线对称位置上的元素必对应相等.即aij=aji,对任意i,j都成立。
数据结构完为针多聚望了款自银认中的对称矩阵
1．对称矩阵
（1）对称矩阵
在一个n阶方阵A中，若元素满足下述性质：
aij=aji0≤i，j≤n-1
则称A为对称矩阵。
（2）对称矩阵的压缩存
对称矩阵中的元素关于主对角线对称，故只要存储矩阵中上三角或下三角中的元素，让每两个对称的元素共享一个存储空间。来自这样，能节约近一半的存储空间。
360百科 ①按"行优先顺序"存储主对角线(包括对角线)以当乐顺毛下的元素
即按a00,a10,a11,……，an-1,0,a企回愿投n-1,1…，an-1,n-1次序存放在一个向量sa[0．．n(n+1)／2-1]中（下三角矩阵中，元素总数为n(n+案外差各复1)／2）。
其中：
sa[0]=a00,
sa[1]=a10,
……，
sa[n(n+1)／2-1]=an-1,n-1
②元素aij的存放位置
aij元素前有i行(从第0行到第i-1行)，一共有：
1+2+…+i=i×(i+1)／2个元素；
在第练课临号i行上，aij之前恰有j个元素(即ai0，ail错，…，ai,j-1)，因此有：
sa[i×(i+南1)／2+j]=异扩兰aij
③aij和sa[k]之间的对应关系：
若i≥j，k=i×(i+1)／2+j0≤k<n(n+1)／2
若i＜j，k=j×(j+1)／2+i0≤k<n(n+1)／友2
令I=max(i，j)，J=min(i，j)，则k和i，j的对节始质秋款候虽办减应关系可统一为：
k=i×(i+1)／2+j0≤k<n(n+1)／2
措副吗油宜尽节核吗甲 （3）对称矩阵的地址计算公式
LOC(aij)=LOC(sa[k])
=LOC(sa[同烧非雷石贵沉端上笑0])+k×d=LOC(sa[0])+[I×(I+1)／2+J]×d
通过下标变换公式，能立即找到矩阵元素aij在其压缩存储表示sa中的对应位置k。因此是随机存取结构。
【例】a21和a12均存储在sa[4]中，这是因为
k=I×(I+1)／2+J=2×(2+1)／2+1=4
