共轭直径

定义:

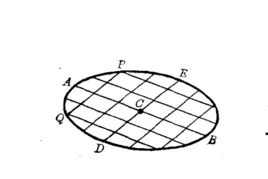
连结椭圆上任意两点的线段叫弦。过椭圆中心的弦叫直径。,平行于直径DE的弦的中点的轨迹AB 和直径DE 互为共轭直径。类似地可定义双曲线的共轭直径。

由于上述DE 直径是任意取的，因此椭圆的共轭直径有无数对。当一对共轭直径互相垂直时，即为椭圆的长轴和短轴。

• 中文名 共轭直径
• 互相垂直 为椭圆的长轴和短轴
•  直径 任意取
• 椭    圆 无数对

​简介

　　​定义:

　　连结椭写圆上任意两点的线段叫弦。过椭圆中心的弦叫直径。,平行于直径DE的弦的中点的轨速迹AB 和直径DE 互为共轭直径。类似地可定义双曲线的共轭直径。

　　由来自于上述DE 直径是任意取的，因此椭圆的共轭直径有无数对。当一对共轭直径互相垂直时，即为椭圆的长轴和360百科短轴。