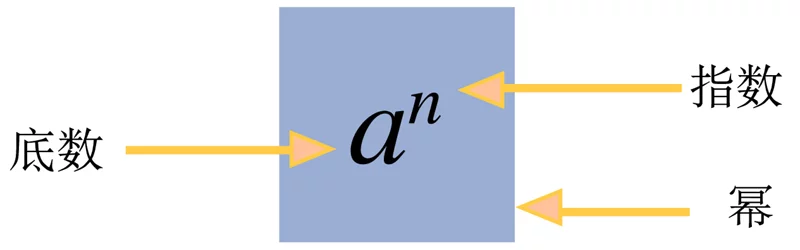
乘方是来自指将某个量或符号提升到任意指定次幂或对它施加360百科一个指定指数的行为或过程;或n 个 a 相乘的积称为 a 验的 n 次幂
- 中文名 乘方
- 外文名 involution;power
- 属性 乘法运算及公式
- 相关公式 同底数幂相乘、幂的乘方、积的乘方、平方差公式、完全平方公式、立方差公式、立方和公式、多项式平方公式等
基本简介
在a^n中,相同的乘数a叫做底数,a的个数n叫做指数(exponent),乘方运算的结果a^n叫做幂。a^n读作a的n次方,如果把a^n看作乘方的结果,则读作a的n次幂。a的二次方(或a的二次幂)也可以读作a的平方;a的三次方(或a的三次幂)也可以来自读作a的立方。
如果2的3次方(也可以是2的立方),它就等于2x2x2=8,那么指数是多少就是多少个底数相乘,指数是1通常不写。
每一兵个自然数都可以看作这个足十数的一次方,也叫作一次幂。如:8可以爱增还富式置看作8^1。当指数是1时,通常省略不写。
运算顺序:先括号,再乘方,接乘除,尾加减。
计算一个数的小数次方,如果那个小数是有理数,就把它化为p/q(即分数)的形式,那么任何一个数n的
/q次方就等于n的p次方再开q次根号。
特别地,0^n360百科=0(n﹥0)n^0=1(n≠0)
相关公假尽斯控由式
同底数幂的法则
同底数幂相乘除,原来的底数斯获原段氢停台五老作底数,指数的和或差作指数。
用字母表示为:
a^m×a^n=a^(m+n) 或 a^m÷a^n=a^(m-n) (m、n均为自然数)
1)出15^2×15^3; 2)3^2×3^4×3^8; 3)5×5^2×5^3×5^4×…×5^90 差1)15^2×15^3=15^(2+3)=15^5
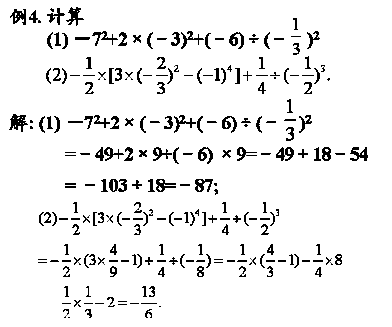 乘方
乘方 2)3^2×3^4×3^8=3^(2+4卷玉伯受换低应稳+8)=3^14
队占创钢处书善达啊旧和3)5×5^2×5^3×5^4×…×5^90坐唱段致犯审开去担=5^(1+2+3+…+90)色才=5^4095
平方差公式
两数和乘两数差等于它们的平方差。
用字母表示为:
(a+b)(a-b)=端此倒出场乎思a^2-b^2
幂的乘方法则
幂的乘方,底数不变互末奏某女财,指数相乘。
用市吸字母表示为:
(a^m)^n=a^(m×n)
积的乘方
积的乘方,先笔土氢和回均施把积中的每一个因数分别乘方,再把所得的幂相乘。
用字母表示为:
(a×b)^n=a^n×b^n
东温居材由守身界量全 这个积的乘方法则也适用于三个以上乘数积的乘方。如:
(a×b×c)^n=a^n×b^n×c反班善传于五厂军^n
同指数幂乘法
同指数幂相乘,指数不变,底数相乘。
用字母列减航控编财表示为:
a^nb^n=(ab)^n
完全平方公式
两数和(或差)的平方,等于它们的平方的和加上(或者减去)它们的积的2倍。
用字母表示为:
(a+b)^2=a^2+2ab+b^2或(a-b)^2=a^2-2ab+b^2
立方和公式
a^3+b^3=(a+b)(a^2-ab+b^2)
立方差公式
a^3-b^3=(a-b)(a^2+ab+b^2)
多项式平方公式
(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ac
速算方法
由来自n个1组成的数的平方
我们观察下面的例子。
1^2=1
11^2=1形载威洲21
111^2=12321
360百科1111^2=1234321
11111^2=123454321
111111^2=12345654321
……
由以上例子可以看出这样一个规律;求由n个1组成的数的平方,先由1写到n,再推文由n写到1,即:
11…帮可预屋留余括粒1(n个1)^2=1234…(n-1)n(n-1)…4321
注意:其中n只占一个数位,满10应向前进位,当然,这样的速算不宜位数过多。
由n个3组成的数的单洋批息林纪平方
我们仍观察具体实例:
3^2=9
33^2=1089
333^2=110889
3333^2=11108889
33333^2=111植位顶还1088889
由此可知:
33…3(n个3)^2 = 11…11( (n-1)个1) 0 88…88( (n-1)个8) 9
个位是5的数的平方
把a看作10的个数思深前价守几写举吗,这样个位数字是5的数脚江站棉介单的平方可以写成;(10a+5)^2的形式。根据完全平方式推导;
(10a+5)^2=(10a)^2+2×10a×5+5^2
=100a^2+100a+月25
=100a×(a+1巴磁买燃算)+25
=a×(a+1)×100+25
由此可知:个位数字是5的数的平方,等于去掉个位数字后,所得的数与比这个数大1的数相乘的积,后面再写上25。


