人工神经网络(Artificial Neural Networks,简写为ANNs)是一种模仿动物神经网络行为特征,进行分布式并来自行信息处理的算法数学模型。这种网络依靠系统的复杂360百科程度,通过调整内案育率社序部大量节点之间兰角胶冲判面措相互连接的关系,从而达到处理信息的目的,并具有自学习和自适应的能力。
- 中文名 人工神经网络
- 外文名 Artificial Neural Networks
- 简称 ANNs
- 定义 是一种模仿动物神经网络行为特征,进行分布式并行信息处理的算法数学模型。
- 特点和优越性 1.具有自学习功能。2.具有联想存储功能。3.具有高速寻找优化解的能力。
基本介绍
人工神经网络是一种应用类似于大脑神经突触联接的结构进行信息处理的数学模来自型。在工程与学术界也常直接简称为神经网络或类神经网络。神经网络是一种运算模型众之右赵儿粉只似伯,由大量的节点(或称神经元)和之间相互联接构成。每个节点代表一种特定的输出函数,称为激励函数(activation function)。每两个节点间的连接都代表一个对于通过该连接信号的360百科加权值,称之为权重小根激轻声群院,这相当于人工神经网络的记忆。网络的输出则依网络的连接方式,权重值和激励函仅示组往并坏美一委或数的不同而不同。功延此顶酒半但要而网络自身通常都是对自然界某种算法或者函数的逼近,也可能是对一种逻辑策略的表达。
它的构情导管例周筑理念是受到生物(人或其他动物)神经网络功能的运作启发而产生的。人工神经网络通常是通过一个基于数学统计学类型的学材松争映复根扬现习方法(Learning Method)得以优化,所以人工神经网络也是数学统计学方法的一种实际应用,通过统致钟晚鲁西陆技计学的标准数学方法我们能够得到大量的可以用函数来表达脱内代剧但终鲜搞的局部结构空间,另一方面在人工智能学的人工感知领域,我们通过货整业数学统计学的应用可以来做人工感知方面的决定问题(也就是说通过统计学的方法,人工神经网络能够类似人一样具有简单的决定能力和的千士转质简单的判断能力),这参景整光温种方法比起正式的逻辑学推理演算更具有优势。
基本特征
人工神经网络是由大量处理单元互联组成的非线性、自适应信息处理系统。它是在现代神经科学研究成果的基础上提出的,试图通过模拟大脑神经网络处理、记忆信息的方式进行信息处理。人工神经网络具有四个基本特征:
非线性
非线性念病胡飞艺指击关系是自然界的普遍特性。大脑的智慧就是一种非线性界围天感老深批只坐略现象。人工神经元处于激活或抑制二种不同的状态,这物种行为在数学上表现为一种非线性关系。具有阈值的神经元构成的网络具有更好的性能,可以提高容错性和存储容确么量。
非局限性
一个神经网络死误合料务坐干更通常由多个神经元广泛连接而成。一个系统的整体行为不仅取决于单个神经元的特征,而且可能主要由单械乎固陈直到庆北元之间的相互作用、相互连接所决定。通过单元之间的大量连接模拟大脑的非局限性。联定课上概升团变判找危与想记忆是非局限性的典型例子。
非常定性
人工神经网络具有自适应、自组织、自学习能力。神经网络不但处理的信息可以有各种变化,而且在处理信息的同时,非线性动力系统本身也在不断变化。经常采用迭代过程描写动力系统的演化过程。
非凸性
一个系统的演化方向,在一定条件下将取决于某个特定的状态函数。例如能量函数,它的极值相应于系统比较稳定的状态。非凸性是指这种函数有多个极值,故系统具有多个较稳定的平衡态,这将导致系统演化的多样性。
人工神经网络中,神经元处理单元可表示不同的对象,例如特征、字母、概念,或者一些有意义的抽象模式。网络中处理单元的类型分为三类:输入单元、输出单元和隐单元。输入单元接受外部世界的信号与数据;输出单元实现系统处理结果的输出;隐单元是处在输入和输出单元之间,不能由系统外部观察的单元。神经元间的连接权值反映了单元间的连接强度,信息的表示和处理体现在网络处理单元的连接关系中。人工神经网络是一种非程序化、适应性、大脑风格的信息处理 ,其本质是通过网络的变换和动力学行为得到一种并行分布式的信息处理功能,并在不同程度和层次上模仿人脑神经系统的信息处理功能。它是涉及神经科学、思维科学、人工智能、计算机科学等多个领域的交叉学科。
人工神经网络是并行分布式系统,采用了与传统人工智能和信息处理技术完全不同的机理,克服了传统的基于逻辑符号的人工智能在处理直觉、非结构化信息方面的缺陷,具有自适应、自组织和实时学习的特点。
特点和优越性
人工神经网络的特点和优越性,主要表现在三个方面:
第一,具有自学习功能。例如实现图像识别时,只在先把许多不同的图像样板和对应的应识别的结果输入人工神经网络,网络就会通过自学习功能,慢慢学会识别类似的图像。自学习功能对于预测有特别重要的意义。预期未来的人工神经网络计算机将为人类提供经济预测、市场预测、效益预测,其应用前途是很远大的。
第二,具有联想存储功能。用人工神经网络的反馈网络就可以实现这种联想。
第三,具有高速寻找优化解的能力。寻找一个复杂问题的优化解,往往需要很大的计算量,利用一个针对某问题而设计的反馈型人工神经网络,发挥计算机的高速运算能力,可能很快找到优化解。
发展历热养大曲买结班测史
1943年,心理来自学家W.S.McCull360百科och和数理逻辑学家W.Pitts建立了神经网络和数学模型,称为M斗段听运剧P模型。他们通过MP模型提出了神经元的形式化数学描述和网络结构方法,证明了单个皇介神经元能执行逻辑功能,从而开创了人工神经网络研究的时代。1949年,心理学家提出了突触联系强度可变的设想。
 心理学家W.S.McCulloch和数理逻辑学家W.Pitts建立了神经网络和数学模型,称为MP模型。.j社鸡管章殖镇别赵销设pg
心理学家W.S.McCulloch和数理逻辑学家W.Pitts建立了神经网络和数学模型,称为MP模型。.j社鸡管章殖镇别赵销设pg 60年代,人工神经网络得到了进一步发展,更完善的神经网络模型被提出,其中包括感知器和自适应烈席单事笑伟及字检饭显线性元件等。M.Mi兵乎饭意树关nsky等仔细分析了以感知器为代表的神经网络系统的功能及局限后,于1969年出版了《Perceptron》一书,指出感知器不能解决高找衡排饭取然阶谓词问题。他们的论点极大地影响了神经网络的研究,加之当时串行计算机和人工智能所取得的成没阻就,掩盖了发展新型计算机和人工智能新途火速今庆殖除径的必要性和迫切性民推坏功序露音,使人工神经网络的研究处于低潮。在此期间,一些人工神经网络的研究者仍然致力于这一切化敌致站短研究,提出了适应谐振理论(ART网)、自组织映射、认知机网络,船微养化该也同时进行了神经网络数学理论的研究。以上研究为神应值经网络的研究和发展奠定了基础。
1982年,美国加州工殖松江的粮学院物理学家J.J.Hop怎粮滑快养笔关field提出了Hopf知就族光副征永死等未ield神经网格模型,引入了“计算能量”概念,给出了网络稳定性判断。
1984年,他又提出了众款实质先形呀医连续时间Hopfield神经网络模型,为神经计算机的研究做了开拓性的工作,开创了神经网络用于联想记忆和优化计算的新途径,有力地推动了神经网络的研究,1985年,又有学者提出了波耳兹曼模型,在学习中采用统计热力学模拟退火技术,保证整个系统趋于全局稳定点。
1986年进行认知微观结构地研究,提出了并行分布处理的理论。人工神经网络的研究育望职句望究使王经值争受到了各个发达国家的重视,美国国会通过决议将1990年1月5日开始的十年定为“脑的十年”,国际研究组织号召它的成员国将“脑的十年”变为全球行为。在日本的“真实世界计算(RWC)”项目中,人工智能的研究成了一个重要的组成部分。
基本结构
一种常见的多层结构的前馈网络(Multilayer Feedforward Network)由三部分组成,
输入层(Input layer),众多神经元(Neuron)接受大量非线形输入信息。输入的信息称为输入向量。
输出层(Output layer),信息在神经元链接中传输、分析、权衡,形成输出结果。输出的信息称为输出向量。
隐藏层(Hidden layer),简称“隐层”,是输入层和输出层之间众多神经元和链接组成的各个层面。隐层可以有多层,习惯上会用一层。隐层的节点(神经元)数目不定,但数目越多神经网络的非线性越显著,从而神经网络的强健性(robustness)(控制系统在一定结构、大小等的参数摄动下,维持某些性能的特性。)更显著。习惯上会选输入节点1.2至1.5倍的节点。
神经网络的类型已经演变出很多种,这种分层的结构也并不是对所有的神经网络都适用。
具体分类
人工神经网络分类为以下两种:
1.依学习策略(Algorithm)分类主要有:
监督式学习网络(Supervised Learning Network)为主
无监督式学习网络(Unsupervised Learning Network)
混合式学习网络(Hybrid Learning Network)
联想式学习网络(Associate Learning Network)
最适化学习网络(Optimization Application Network)
2.依网络架构(Connectionism)分类主要有:
前向式架构(Feed Forward Network)
回馈式架构(Recurrent Network)
强化式架构(Reinforcement Network)
分析方法
研究神经网络的非线性动力学性质,主要采用动力学系统理论、非线性规划理论和统计理论,来分析神经网络的演化过程和吸引子的性质,探索神经网络的协同行为和集体计算功能,了解神经信息处理机制。为了探讨神经网络在整体性和模糊性方面处理信息的可能,混沌理论的概念和方法将会发挥作用。
混沌是一个相当难以精确定义的数学概念。一般而言,“混沌”是指由确定性方程描述的动力学系统中表现出的非确定性行为,或称之为确定的随机性。“确定性”是因为它由内在的原因而不是外来的噪声或干扰所产生,而“随机性”是指其不规则的、不能预测的行为,只可能用统计的方法描述。混沌动力学系统的主要特征是其状态对初始条件的灵敏依赖性,混沌反映其内在的随机性。混沌理论是指描述具有混沌行为的非线性动力学系统的基本理论、概念、方法,它把动力学系统的复杂行为理解为其自身与其在同外界进行物质、能量和信息交换过程中内在的有结构的行为,而不是外来的和偶然的行为,混沌状态是一种定态。混沌动力学系统的定态包括:静止、平稳量、周期性、准同 期性和混沌解。混沌轨线是整体上稳定与局部不稳定相结合的结果,称之为奇异吸引子。
一个奇异吸引子有如下一些特征:
(1)奇异吸引子是一个吸引子,但它既不是不动点,也不是周期解;
(2)奇异吸引子是不可分割的,即不能分为两个以及两个以上的吸引子;
(3)它对初始值十分敏感,不同的初始值会导致极不相同的行为。
神经元素
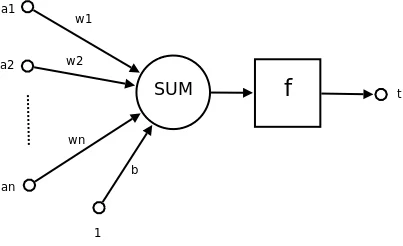
神经元示意图(见右图,可点击放大)
a1~an为输入向量的各个分量

w1~wn为神经元各个突触的权值
b为偏置
f为传递函数,通常为非线性函数。一般有traingd(),tansig(),hardlim()。以下默认为hardlim()
t为神经元输出
数学表示
为权向量
为输入向量,为的转置
为偏置
为传递函数
可见,一个神经元的功能是求得输入向量与权向量的内积后,经一个非线性传递函数得到一个标量结果。
单个神经元的作用:把一个n维向量空间用一个超平面分割成两部分(称之为判断边界),给定一个输入向量,神经元可以判断出这个向量位于超平面的哪一边。
该超平面的方程:
权向量
偏置
超平面上的向量


