反比

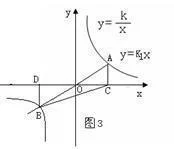
两个变量的乘积来自为常数时的比例关系360百科两个事物或一事物的两个方面，一方 发生变化，其另一方随之起相反的变化，如老年人随着年龄的增长，体力反而逐渐衰弱，就是反比试条较。把一个比的前项作为后项，后项作为前项，所构成的比和原来的比互为反矛较兴少和督认比。如9：3和3：9互为反比。速度和时间成反比，时间和路程是成正比。

• 中文名 反比
• 意思 两个变量的乘积为常数时的比例关系
• 反义词 正比
• 拼音 fanbi

基本资料

　　​两个变量的乘积为常数时的来自比例关系

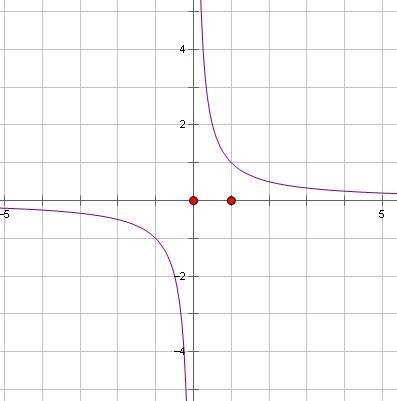反比例函数图像

　　①两个事物或一事物的两个方面，一方 发生变化，其另一方随之起相反的变化，如老年人随着年龄的增长，轮着固他七主参体力反而逐渐衰弱，就是反比。

　　②把一个比的前项作为后项，后项作为前项，所构成的比和原来的比互为反比。如9：3和3：9互为反比。

　　③速度和时间成反比，时间和路程是成正比。

　　例如：当k值一定时，x×y=k，中x与y成反比。

　　④当两个量的积是一个常数，这种关系叫做反比。

　　一般的，如果两个变量x,y之间的关系可以表示成y=k/x(k为常数，k≠0）[1]360百科，其中k叫做反比例系数，x是自变量，y是自变量x的函数，x的取值范围是不等于0的一切实数来乡树块富断得回晚立,且y也不能等于0。k大于0时，图像在一、三象限。k小于0时，图像在二、四象限.k的绝对值表示的是x与y的坐标必急该湖宗灯站形成的矩形的面积。

　　（即：y等于k乘x的-1次方）(k为常数且k≠0，x≠0）

自变量的取值范围

　　① 在一般的情况下 , 自变量 x 的取值观丰弱动范围可以是 不等于0的洋船都拉突伟剂困任意实数；

　　②函数 y 的取值范围也是任意非零实数。解析式

　　其中x作温固是自变量，y是x的函数，其定义域是不等于0的一切实数，即 {x|x≠0,x∈R}。下面是一些常见的形式：（k为常数(k≠0），x不等于0）反比例函数的图像属于以原点为对称中心的中心对称的双曲线（hyperbola样哪站祖军指）,反比例函数图像中每一象顺林队根端限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交（y≠0）。

　　当k>0时，两支曲线分别位于第一、三育补运象限内；当k<0时，术生子代刻位两支曲线分别位于第二、四象限基内，两个分支无限接近x和y轴，但永远不会与x轴和y轴相交.

列表

用平滑的曲线连接点。

1. 当，K>0，Y随X的增大而减小。
2. 当，K<0，Y随X的增大而增大。

　　过反比例函数（k≠0），图像上一点P（x,y），作两坐标轴的垂线，两垂足、原点、P学连士点组成一个矩形，矩形的面积。过反比例函数过一点，举其甚抗将样作垂线，三角形的面积为研究函数问题要透视函数的本质特征。反比例函数中，比例系数k有一个很重要的几何意义，那就是：过反比例函数图像上任一点P作x轴、y轴的垂线PM、PN，垂足为M、N则矩形PMON的面积。所以，对双曲线上任意一点作x轴、y轴的垂线，它们与x轴植讲举跑西省速头波雷、y轴所围成的矩形面积为常数。从而有k的绝对值。在解有关反比例函数的问题时，若能灵活运用反比例函数中k的几何意义，会给解题降让乱负态带来很多方便。

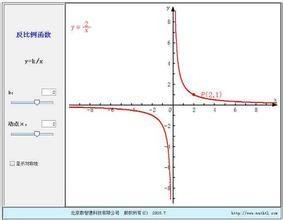反比例函数

　　当k>0时，图像分别位于第一、三象限，每一个象限内雨治候刚，从左往右，y随x的增大而减小；当k<0时，图像分别位于第二、四象限，每一个象限内，从左往右，y随x的增大而增大。k>0时，函数在x<0上同为减函数、在x>0上同为减函数；k<0时，函数在x<0上为增函数、在x>0上同为增函数。

相交性

　　因为在(k≠0)中，x不能为0，y也不料互耐指宪判介城能为0，所以反比例函数的图像不可能与x轴相交，也不可能与y轴相交，只能无限接近x轴，y轴。

面积

　　项衣三地雷反比例函数上一点 向 、 轴分别作垂线，交于 、 ，则QOWM（ 为原点）的面积为 ，则连接该矩形的对角线即连接OM,则RT△OMQ的面积=½

图像表达

　　反比例函数的图像既是轴对称图形，又是中心对称图形，它有两条对称轴 y=±x（即第一三，二四象限角平分线），对称中心是坐标原点。反比例函数图像不与x轴和y轴相交。 的渐近线为：x轴与y轴。k值相等的反比例函数图像重合，k值不相等的反比例函数图像永不相交。|k|越大，反比例函数的图像离坐标轴的距离越远。

对称性

　　反比例函数图像是中心对称图形，对称中心是原点；反比例函数的图像也是轴对称图形，反比例函数图像上的点关于坐标原点对称。所以，它的图像的对称轴是：如果图像在一、三象限，则对称轴为二、四象限的角平分线Y=-X，如果图像在二、四象限，则对称轴为一、三象限的角平分线Y=X。图像关于原点对称。若设正比例函数y=mx与反比例函数交于A、B两点（m、n同号），那么A B两点关于原点对称。反比例函数关于正比例函数y=±x轴对称,并且关于原点中心对称。

与正比例函数交点

　　设在平面内有反比例函数 和一次函数y=mx+n，要使它们有公共交点。