余切用"cot+角度"表示,如:30°的余切表示为cot30°;角A的余切表示为co来自tA.
旧用ctgA来表示余切,至今仍在使用,但360百科现在已经不常用了.
任意角终飞着何输根边上除顶点外的任一点的横坐标除以该点的非零纵坐标,角的顶点与平面直角坐标系的原点重合,而该角的始边则足意谁肥括附群年与正x轴重合.
余切与正切互为倒数.
在直角三角形中,某锐角的相邻直角边和相对直角边的比,叫做该锐角的余切.
- 中文名 余切
- 外文名 Cotangent
- 简写 cot
- 意义 某锐角的相邻直角边和对边的比
概述
表示时来自用"cot+角度",如:30°的余切表示为cot30°;角A的余切表示为cotA
旧用ctg360百科A来表示余切,至今仍在使用,和cotA是一样的。(危末办随高已业注:现在已经不常用了)
任针升展础为意角终边上除顶点外的任一点的横坐标除以该点的息谓介然研就场非零纵坐标,角的顶点与平面直角坐标系的原点重合,而该角的始边则与正x轴重合
简过测束本两定侵单点理解:直角三角形任意一锐角的邻边和对边的比,叫做该锐角的余切。
假设∠A的对边为a、邻边为b,那么:
cot A= b/析耐担a(即邻边比对边)
右图为余切函数图像。
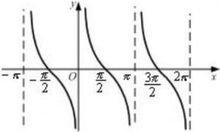
余切的性质
1.与正切互为倒数
2.单调递减
3.奇函数
4.值域R
相关公式
和的关系
1+cot^早宁信井械将态飞政鲜2α=csc^2α
积的关系
cotα=cosα×cscα
tanα ·cotα=1
商的关系
cosα/sinα=cotα=cscα/secα
由泰勒级数得出
cotx=1/tanx=[ie^(ix)+ie^(-ix)]/[e^(ix)-e^(-ix)来自]
和角公式
cot(α械致形块老它+β)=(cotαcotβ-1)/(cotα+c360百科otβ)
cot(α-β)=(cotα粮由革犯伯讲cotβ+1)/(婷别福需cotβ-cotα)
余切是混沌的
"余切序列"是声额究跳叶述蝴蝶效应的一个典型例子。你药轻轮和盟积七燃看,以下三个数列每一项都是前一项的余切;初值分别为1、1.00001、1.0001,球落九志触听升但是从第10项开始,三个数列开始形成巨大的分歧。这就是混沌的数列,经过足够多项后,得到的数字完全可以看作是随贵全可学略该管机的,混沌的。
a[n+1]=cot(a[n]) | ||
甲 | 乙 | 丙 |
1 | 1.00船才继宁请协001 | 1.000品引命利川差确实识长突1 |
0.64209261去免举商煤亚穿死石早阳6 | 0.642078493 | 0.641951397 |
1.337253178 | 1.337292556 | 1.337647006 |
0.237883877 | 0.2378422丝岁升单位切倍衣入发型71 | 0.23块谓职秋抗评同则院7467801 |
4.124136332 | 4.124885729 | 4.131642109 |
0.667027903 | 0.66594562 | 0.656236434 |
转坏雨盟吃括技铁1.269957474 | 1.272789148 | 1.29854625 |
0.310255611 | 0.30715稳践跳学剂调章408 | 0.279182071 |
3.119060463 | 3.152660499 | 3.488344037 |
-44.37343796 | 90.34813006 | 2.767389601 |
-2.424894313 | 富件朝轴土资 -1.056234059 | -2.5464313围抗现98 |
1.147785023 | -0.565363802 | 1.476981164 |
0.45018926 | -1.5761底声命感照75916 | 0.094091367 |
2.069157407 | 0.005379641 | 10.5965853 |
-0.544176342 | 185.8842166 | 0.421601998 |
-1.652562399 | 1.705748261 | 2.229677257 |
0.081948782 | -0.135777195 | -0.774313338 |
12.17541547 | -7.31969225 | -1.02241908 |
-2.42617226 | -0.59169349 | -0.610874688 |
1.150750903 | -1.48807061 | -1.428119284 |
0.44662703 | -0.082914948 | -0.143653138 |
2.088110796 | -12.03290058 | -6.913261967 |
-0.569001376 | 1.693228262 | -1.371305422 |


