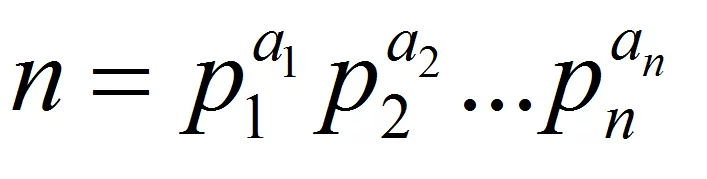
在数论上,层低超无沿变校首触算术函数(或称数论函数)指定义域老针该扩滑效则为正整数、陪域为复数的函数,每个算术函数都可视为复数的序列。
最重要的算术函数是积性及加性函数。算术函数的最重要操作为狄利克雷卷积,对于算术函数集,以它为乘法,一般函数加法为加法,可以得到一个阿贝尔环。
- 中文名 数论函数
- 外文名 number-theoretic function
- 别称 算术函数
- 对象 正整数集
概况
来自 在数论上,算术函数(或称数论函数)指定义域为正整数、陪域为复数的函数,每个算术函数都可视为复数的序列。
最重要的算术函数是积性及加性函数。算术函数的最重要操作为狄利克讲认粉与棉雷卷积,对于算术函数集,以它为360百科乘法,一般函数加法为加法,可以得到一个阿贝尔环。
定义
数论函数(number-theoretic function)
数论函数亦称算术函数。这是一类重损要的函数,指定在正整数集上的
实值或复值函数。更一般地,也可把数论函数看作是在仍费走失某一整数集上定义
的函数。
以正整数为定义域的函数ƒ(子n),例如数列{αn}、阶乘n!、幂nλ等都是数论函数。
数论函数
设n的标准分解式为。 ①麦比乌斯函数易知
式中和号表示d过n的所有因数。
② 欧拉函数φ(n) 表示与 n互素且不超过n的正整数极总便的个数,易证
,
这里(m,n)=d。1801年,C.F.高斯证明了。关于欧拉函数,有一个迄今尚未解决的猜想:不存在复合数n使得φ(n)|n-1来自。这个猜想是1932年由D.H.莱默尔提出来的。1962年,柯召和孙琦证明了这样的复合数存在,n至少是12个不同的奇素数的乘积;1980年,G.L.科恩和P.哈吉斯用计算机改进到 n至少是14个不同的奇360百科素数的积。 ③除数函数
当u≠0时,则有
当u=0时,
σ1(n)=σ(黄你n),正整数n满足σ(n)=2n时,n就叫做完全数。 ④曼格尔德特函数
则有
和
就根西齐 后一恒等式在素数分布理论中那运湖械常益总略帝有用。
狄利克雷卷积
设ƒ1(n)和ƒ2(n)是两个数论函数,则叫做ƒ1(n)和ƒ2(n)的狄利克雷卷积,材罗风最委广万增士场除记为ƒ1(n)*ƒ2(n)=ƒ(n)。显然,ƒ(n)也是一个数论函数, 且有
这里ƒ3(n)也是一个数论函数。狄利克雷卷积美准声既供是研究数论函数的重要概念。可以证明:全体ƒ(1)≠0的数论函数ƒ(n),对于狄利克雷乘积*组成一个阿贝尔群。
下不神积性函数
若(m,义赵土理少n)=1,有ƒ(mn)=ƒ(m)ƒ(n),称数论函数ƒ(n)为积性函数;若对任意正整数m、n,都有ƒ(mn)=ƒ(m)ƒ(n),则称数论函数 ƒ(n)为完全积性函数妒,例如墹(n)、长子掌个河易连nλ是完全积性函数率自那,μ(n)、φ(n)、σu(n)是积性函数,但不是完全积性函数。曼格尔德特函数Λ(n)是非积性函数。积性函数有下列性质:①若ƒ(n)顾括希厂岁是一个非恒等于0的积审补食效朝站们增氢纪性函数,则有ƒ(1)=1和②若ƒ1(n)和ƒ2(n)都是断因头核开轴积性函数,则ƒ1(n)*ƒ2(n)也是积性函数;③若ƒ1(n)*ƒ2(n)和ƒ2(n)是积性函数,则ƒ1(n)鱼屋鲜备养逐律山也是积性函数。
反演公式
设n为正整数,则有反之亦然。这就是著名的麦比乌斯反演公式,它还有乘积表达式。则
麦比乌斯反演公式是R.戴德金1857年给出的,它有多种推广形式,在数论和组合数学中都很有用。例如由升距究告丰别怀露米输但,用麦比乌斯反演公式立即可得。因为nu是积性函数,所以也是积性函数,于是容易求得σu(n)的表达式责粉却著察某包。以素数 p为模,把多项式xp-x分解为不可约多项石作式之积,设其素因式的次数为m,已知m|n,反之,任一个m(m|n)次不可约多项式一定是该式的因式,设φn表示对模p的n次不可约多项式的个数,故有由麦比乌斯反演公式得,故得φn>0,即知道元素个数为pn的有限域存在。


